流体仿真
本文部分内容为 Physics-Based Simulation & Animation of Fluids (by Chand T. John, Ph.D)的中文翻译。本文所涉及的所有代码以 该 License 发布。
Part of this article is the Chinese translation of Physics-Based Simulation & Animation of Fluids by Chand T. John, Ph.D. This article is published under This License.
This product includes software developed by Chand John.
This product includes software developed by the University of Maryland, Baltimore County.
基于粒子的流体模拟方法
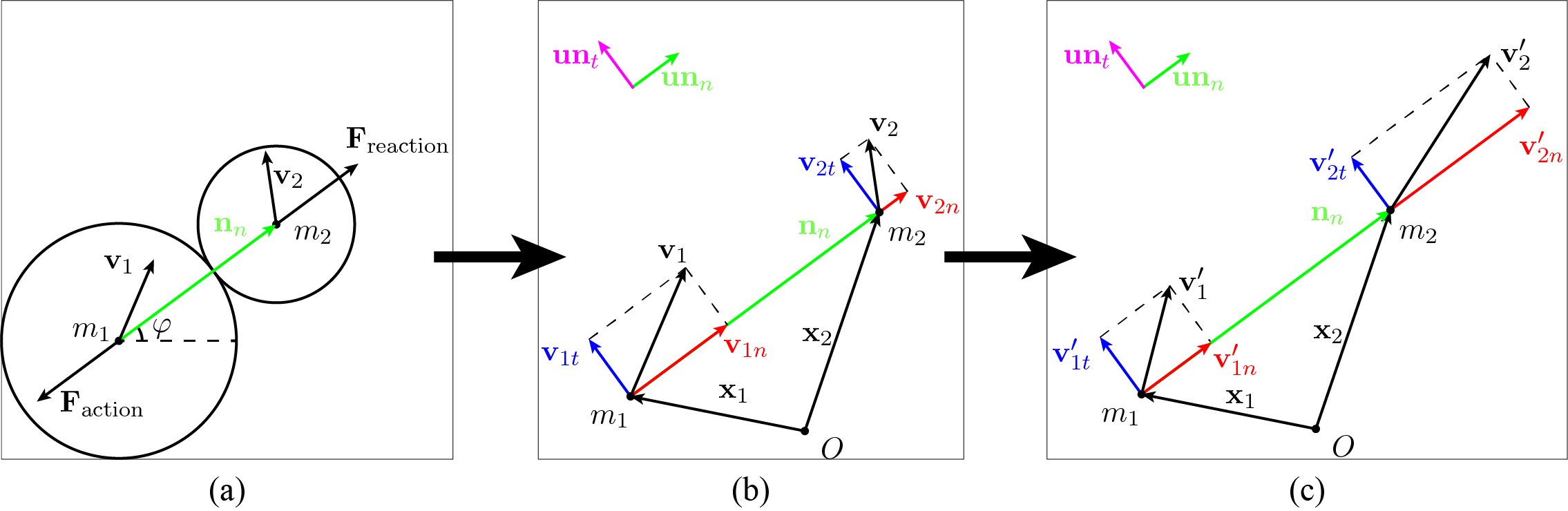
二维完全弹性斜碰的末速度
假设我们具有一定的数理基础,了解一些经典物理学的基本原理:
牛顿第一定律(Newton’s First Law of Motion)
物体在不受外力作用时,保持静止或匀速直线运动状态,直到有外力迫使其改变运动状态.
动量守恒定律(Law of Conservation of Linear Momentum)
不受合外力,或合外力为 \(0\) 的系统动量守恒,即
\[\mathbf{F}_{\text{net force}}=\mathbf{0} \rightarrow \sum_{i} \mathbf{p}_{i} = \sum_{i} \mathbf{p}^\prime_{i}\]其中 \(\mathbf{p}_{i}\) 为物体 \(i\) 的初动量,\(\mathbf{p}_{i}^\prime\) 为物体 \(i\) 的末动量.
能量守恒定律(Law Conservation of Energy)
封闭系统的能量守恒.
质量守恒定律(Law Conservation of Mass)
封闭系统的质量守恒.
质量分别为 \(m_1\), \(m_2\) 的两个均匀小球 \(a\) 与 \(b\) 在时刻 \(t\) 碰撞. 此时,两小球的质心分别位于 \(\mathbf{x}_1\) 与 \(\mathbf{x}_2\),瞬时速度分别为 \(\mathbf{v}_1\) 与 \(\mathbf{v}_2\). 碰撞的法向单位向量为
\[\mathbf{un}_n=\frac{\mathbf{n}_n}{\left\|\mathbf{n}_n\right\|}\]单位切向量为
\[\mathbf{un}_t=\frac{\mathbf{n}_t}{\left\|\mathbf{n}_t\right\|}\]其中
\[\left\{ \begin{aligned} \mathbf{n}_n &= \mathbf{x}_1 - \mathbf{x}_2 = \begin{pmatrix} x_{1x} - x_{2x} \\ x_{1y} - x_{2y} \\ \end{pmatrix} \\ \mathbf{n}_t &= \begin{pmatrix} x_{1y} - x_{2y} \\ x_{2x} - x_{1x} \\ \end{pmatrix} \\ \end{aligned}\right.\]在碰撞瞬间,小球的碰撞力极大,因此可视作整个系统不受合外力作用,系统的动量守恒:
\[\begin{align} m_1 \mathbf{v}_1 + m_2 \mathbf{v}_2 &= m_1 \mathbf{v}_1^\prime + m_2 \mathbf{v}_2^\prime \\ m_1 \left(\mathbf{v}_1-\mathbf{v}_1^\prime\right) &= m_2 \left(\mathbf{v}_2^\prime-\mathbf{v}_2\right) \tag{1} \\ \end{align}\]即
\[\left\{ \begin{aligned} m_1 \left(v_{1n}-v_{1n}^\prime\right) &= m_2 \left(v_{2n}^\prime-v_{2n}\right) \\ m_1 \left(v_{1t}-v_{1t}^\prime\right) &= m_2 \left(v_{2t}^\prime-v_{2t}\right) \\ \end{aligned}\right. \tag{2}\]在碰撞的法向上,系统合外力为 \(0\),机械能守恒:
\[\begin{align} \frac{1}{2}m_1 v_{1n}^2 + \frac{1}{2}m_2 v_{2n}^2 &= \frac{1}{2}m_1 (v_{1n}^\prime)^2 + \frac{1}{2}m_2 (v_{2n}^\prime)^2 \\ m_1 \left(v_{1n}^2-(v_{1n}^\prime)^2\right) &= m_2 \left((v_{2n}^\prime)^2 - v_{2n}^2\right)\\ m_1 \left(v_{1n}-v_{1n}^\prime\right)\left(v_{1n}+v_{1n}^\prime\right) &= m_2 \left(v_{2n}^\prime-v_{2n}\right)\left(v_{2n}^\prime+v_{2n}\right) \tag{3}\\ \end{align}\]在碰撞的切向上,系统不受力,有:
\[\left\{ \begin{aligned} v_{1t}^\prime &= v_{1t} \\ v_{2t}^\prime &= v_{2t} \\ \end{aligned}\tag{4}\right.\]令 \((3)/(2)\),有:
\[v_{1n}+v_{1n}^\prime=v_{2n}^\prime + v_{2n}\]又有 \((4)\),得:
\[\mathbf{v}_1^\prime - \mathbf{v}_2^\prime = \begin{pmatrix} v_{2n} - v_{1n} \\ v_{1t} - v_{2t} \\ \end{pmatrix}\]可以得到 \(\mathbf{v}_1^\prime\):
\[\mathbf{v}_1^\prime = \mathbf{v}_2^\prime + \begin{pmatrix} v_{2n} - v_{1n} \\ v_{1t} - v_{2t} \\ \end{pmatrix} \tag{5}\]将 \((5)\) 代入 \((1)\) 中,有
\[\begin{align} m_1 \left(\mathbf{v}_1-\mathbf{v}_2^\prime + \begin{pmatrix} v_{2n} - v_{1n} \\ v_{1t} - v_{2t} \\ \end{pmatrix}\right) - m_2 \left(\mathbf{v}_2^\prime-\mathbf{v}_2\right) = 0 \\ m_1 \left(\mathbf{v}_1-\mathbf{v}_2^\prime +\begin{pmatrix} \langle\mathbf{v}_2 - \mathbf{v}_1, \mathbf{un}_n \rangle \\ \langle\mathbf{v}_2 - \mathbf{v}_1, -\mathbf{un}_t \rangle \\ \end{pmatrix} \right) - m_2 \left(\mathbf{v}_2^\prime-\mathbf{v}_2\right) = 0 \\ (m_1+m_2)\mathbf{v}_2^\prime = m_2\mathbf{v}_2 + m_1\mathbf{v}_1 - m_1\begin{pmatrix} \langle\mathbf{v}_2 - \mathbf{v}_1, \mathbf{un}_n \rangle \\ \langle\mathbf{v}_2 - \mathbf{v}_1, -\mathbf{un}_t \rangle \\ \end{pmatrix}\\ \end{align}\]得
\[\begin{align} \mathbf{v}_2^\prime &= \frac{1}{m_1+m_2}\left( m_2\mathbf{v}_2 + m_1\mathbf{v}_1 - m_1\begin{pmatrix} \langle\mathbf{v}_2 - \mathbf{v}_1, \mathbf{un}_n \rangle \\ \langle\mathbf{v}_2 - \mathbf{v}_1, -\mathbf{un}_t \rangle \\ \end{pmatrix}\right)\\ &= \frac{1}{m_1+m_2}\left( (m_1+m_2)\mathbf{v}_2 + m_1 (\mathbf{v}_1-\mathbf{v}_2) - m_1\begin{pmatrix} \langle\mathbf{v}_2 - \mathbf{v}_1, \mathbf{un}_n \rangle \\ \langle\mathbf{v}_2 - \mathbf{v}_1, -\mathbf{un}_t \rangle \\ \end{pmatrix}\right)\\ &= \mathbf{v}_2 - \frac{m_1}{m_1+m_2}\left(\begin{pmatrix} \langle\mathbf{v}_2 - \mathbf{v}_1, \mathbf{un}_n \rangle \\ \langle\mathbf{v}_2 - \mathbf{v}_1, \mathbf{un}_t \rangle \\ \end{pmatrix} + \begin{pmatrix} \langle\mathbf{v}_2 - \mathbf{v}_1, \mathbf{un}_n \rangle \\ \langle\mathbf{v}_2 - \mathbf{v}_1, -\mathbf{un}_t \rangle \\ \end{pmatrix}\right)\\ &= \mathbf{v}_2 - \frac{2m_1}{m_1+m_2}\langle\mathbf{v}_2-\mathbf{v}_1, \mathbf{n}_n\rangle\frac{\mathbf{n}_n}{\left\|\mathbf{n}_n\right\|^2}\\ &= \mathbf{v}_2 - \frac{2m_1}{m_1+m_2}\frac{\langle\mathbf{v}_2-\mathbf{v}_1, \mathbf{x}_2-\mathbf{x}_1\rangle}{\left\|\mathbf{x}_2-\mathbf{x}_1\right\|^2}(\mathbf{x}_2-\mathbf{x}_1)\\ \end{align}\]同理可得 \(\mathbf{v}_1^\prime\),综上
\[\left\{\begin{aligned} \mathbf{v}_1^\prime &= \mathbf{v}_1 - \frac{2m_2}{m_1+m_2}\frac{\langle\mathbf{v}_1-\mathbf{v}_2, \mathbf{x}_1-\mathbf{x}_2\rangle}{\left\|\mathbf{x}_1-\mathbf{x}_2\right\|^2}(\mathbf{x}_1-\mathbf{x}_2)\\ \mathbf{v}_2^\prime &= \mathbf{v}_2 - \frac{2m_1}{m_1+m_2}\frac{\langle\mathbf{v}_2-\mathbf{v}_1, \mathbf{x}_2-\mathbf{x}_1\rangle}{\left\|\mathbf{x}_2-\mathbf{x}_1\right\|^2}(\mathbf{x}_2-\mathbf{x}_1)\\ \end{aligned}\right.\]二维完全弹性斜碰的相互作用力
牛顿第三定律(Newton’s Third Law of Motion)
对于任意两个物体之间的相互作用,作用力与反作用力大小相等,方向相反,即
\[\mathbf{F}_{\text{action}}=-\mathbf{F}_{\text{reaction}}\]冲量-动量定理(Impulse-Momentum Theorem)
物体动量的变化与其作用力在时间上的积分(即冲量)相等,即
\[\begin{align} \mathbf{J} = \int_0^t\mathbf{F} \mathrm{d}t &= \Delta \mathbf{p} \\ &= m\Delta \mathbf{v} \end{align}\]由冲量-动量定理与牛顿第三定律,有弹性碰撞时球 \(a\) 作用于 球 \(b\) 的作用力
\[\begin{align} \int_0^t \mathbf{F}_{\text{action}} \mathrm{d}t &= m_1(\mathbf{v}_1^\prime-\mathbf{v}_1) \\ &=\frac{2m_2}{m_1+m_2}\frac{\langle\mathbf{v}_1-\mathbf{v}_2, \mathbf{x}_1-\mathbf{x}_2\rangle}{\left\|\mathbf{x}_1-\mathbf{x}_2\right\|^2}(\mathbf{x}_1-\mathbf{x}_2)\\ \end{align}\]由于碰撞时间极短,\(\mathbf{F}_{\text{action}}\) 在 碰撞时间 \(\Delta t\) 内可视为恒定值,有
\[\mathbf{F}_{\text{action}} = \frac{1}{\Delta t}\frac{2m_2}{m_1+m_2}\frac{\langle\mathbf{v}_1-\mathbf{v}_2, \mathbf{x}_1-\mathbf{x}_2\rangle}{\left\|\mathbf{x}_1-\mathbf{x}_2\right\|^2}(\mathbf{x}_1-\mathbf{x}_2)\]与反作用力
\[\mathbf{F}_{\text{reaction}} = \frac{1}{\Delta t}\frac{2m_1}{m_1+m_2}\frac{\langle\mathbf{v}_2-\mathbf{v}_1, \mathbf{x}_2-\mathbf{x}_1\rangle}{\left\|\mathbf{x}_2-\mathbf{x}_1\right\|^2}(\mathbf{x}_2-\mathbf{x}_1)\]二维完全弹性斜碰的加速度
牛顿第二定律(Newton’s Second Law of Motion)
物体的加速度与所受的合外力成正比,与物体的质量成反比,即
\[\mathbf{F}_{\text{net force}}=m\mathbf{a}\]其中 \(\mathbf{F}_{\text{net force}}\) 为物理所受的合外力,\(m\) 为物体质量,\(\mathbf{a}\) 为物体的加速度.
小球 \(a\) 的加速度为
\[\begin{align} \mathbf{a}_1 &= \frac{\mathbf{F}_{\text{action}}}{m_1} \\ &= \frac{1}{m_1\Delta t}\frac{2m_2}{m_1+m_2}\frac{\langle\mathbf{v}_1-\mathbf{v}_2, \mathbf{x}_1-\mathbf{x}_2\rangle}{\left\|\mathbf{x}_1-\mathbf{x}_2\right\|^2}(\mathbf{x}_1-\mathbf{x}_2) \end{align}\]二维完全弹性斜碰的速度更新
我们知道,时刻 \(t\) 的速度(velocity) \(\mathbf{v}(t)\) 是位置函数 \(\mathbf{x}(t)\) 对时间的一阶导数,即
\[\mathbf{v}(t) = \frac{\mathrm{d}}{\mathrm{d}t}\mathbf{x}(t)\]而时刻 \(t\) 加速度(acceleration) \(\mathbf{a}(t)\) 是位置函数 \(\mathbf{x}(t)\) 对时间的二阶导数,即
\[\mathbf{a}(t) = \frac{\mathrm{d}^2}{\mathrm{d}t^2}\mathbf{x}(t)\]假设小球只在发生弹性碰撞时受力,使该时刻的加速度发生改变,其余时刻加速度为 \(\mathbf{0}\). 则此时加速度函数 \(\mathbf{a}(t)\) 是已知的,则有
\[\mathbf{v}(t) = \int_0^t \mathbf{a}(x) \mathrm{d}x\]相当于小球的位置函数可计算:
\[\mathbf{x}(t) = \int_0^t \mathbf{v}(x) \mathrm{d}x\]假设时间间隔 \(\Delta t\) 极短,\(\mathbf{a}(t)\) 可视作常量,有
\[\begin{align} \mathbf{v}(t+\Delta t) &= \mathbf{v}(t) + \Delta \mathbf{v} \\ &= \mathbf{v}(t) + \mathbf{a}(t)\Delta t \\ \end{align}\]则有
\[\begin{align} \mathbf{x}(t+\Delta t) &= \mathbf{x}(t) + \Delta \mathbf{x} \\ &= \mathbf{x}(t) + \mathbf{v}(t)\Delta t \\ \end{align}\]即可更新小球的位置 \(\mathbf{x}\).